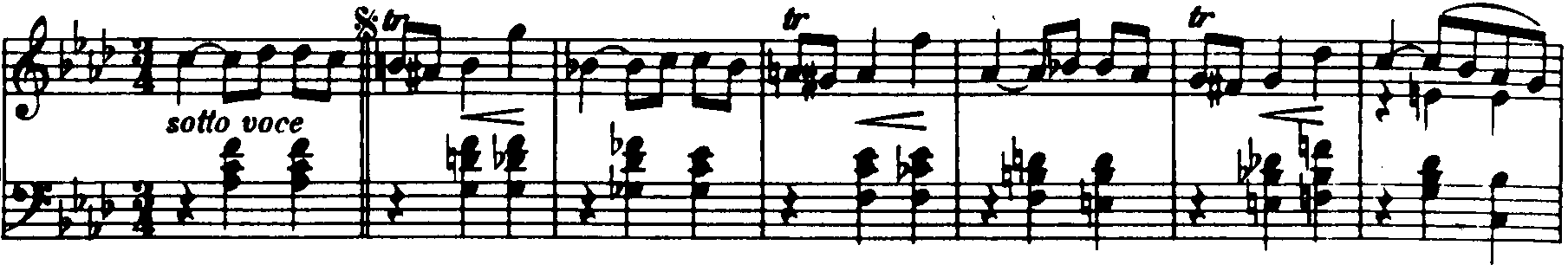
Up to this point, the harmonic materials we've studied have all been based on functional harmonic progression (with the exception of a few embellishing chords). This means that the chords we've identified have all been expected to behave in a certain manner, usually with the goal of leading to a dominant, and ultimately a tonic, chord. An example of this type of functional progression would be:
f: ii viio6 V VI N6 V7 i iv6 Fr+6 V
One point in this progression is interesting to note: the motion from iv6 to the Fr+6 chord. In this example, the iv6 would contain a Db in the bass and Bb in one of the upper voices. The Bb would probably progress chromatically through B (natural) (in the Fr+6 chord) to C as part of the V chord. The Fr+6 chord is created through the linear chromatic motion of the voice containing the B (natural). Although it serves a functional purpose, the Fr+6 chord is produced through linear means. This is an isolated example of linear harmony, a chord created through linear chromatic motion in one or more voices.
As the use of chromaticism became more prevalent during the nineteenth century, so did the occurrence and extent of linear progressions. Not simply one or two chords, but the harmonic material of entire phrases or sections would be based on linear motion.
The following example is the first seven measures of Mazurka 49 in F minor, Op. posth. 68, no. 4, by Chopin.
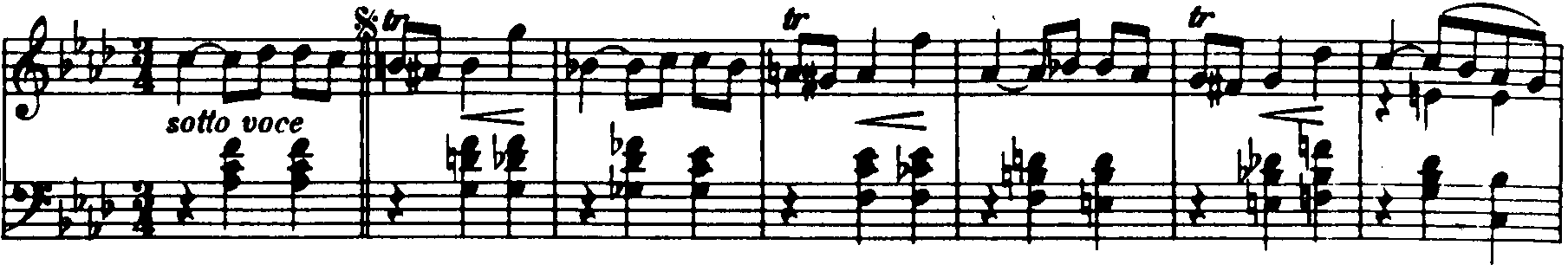
Note that the primary harmonic motion of this phrase is from the tonic chord in m. 1 (i6) to the dominant in m. 7 (followed by resolution to tonic in m. 8). How that motion to the dominant is accomplished is rather interesting. As the example below illustrates, note that starting in m. 2 each voice (including the melody) begins a chromatic descent, stopping in the middle of m. 6.
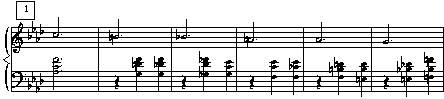
When analyzing such linear motions, at least two things are important to note: 1) the "pillar" chords (starting and ending chords), these chords will be functional in the key, and 2) what techniques are used in getting from the first to the last chord. The only roman numerals that need to be supplied should be the first and last chords. It will usually be very difficult, if not impossible, to determine roman numerals for the linear chords ( and since RN's imply function, and these chord aren't functional, it's usually not worth the effort). What you can do, and this is often very interesting, is determine the root and quality of the linear chords using jazz chord symbols. The following bassline reduction illustrates this technique.

As you view the succession of chord roots, something interesting appears. There seems to be a circle of fifths connection - G (Gb) C F B E . While this pattern does appear, the linear motion from chord to chord disguises the functional possibilities, so what you really hear is the descending chromatic motion gradually changing the sonorities.
The entire Chopin Mazurka is reprinted on the following page. Note that this passage of linear harmony is combined with passages of very clear functional relationships such as mm. 15-23. For another discussion of a portion of this same work, read Turek, vol. 2, pp. 242-243. The term Turek uses is "Chord Mutation". I would rather avoid this term since we use the word "mutation" for another type of phenomenon. Aside from the example above, and the passage Turek discusses, this Mazurka contains one more example of a passage based on linear harmony. See if you can find it, and create a reduction similar to the previous example illustrating the linear motion and functional purpose.

