
Chromatic modulation
(o7, +6, N6 chords as pivot chords)
The fully-diminished seventh chord, the augmented sixth chord (most especially the Gr+6), and the Neapolitan sixth chord may all be used as pivot chords in modulations. This handout describes the process for all three; the o7 chord is by far the most complicated.
The o7 as a pivot chord
This portion of the handout is divided into five basic sections: 1) a brief introduction showing the versatility of the o7 as a pivot chord; 2) an explanation of how, given a single o7 chord, one may modulate anywhere; 3) a discussion of how to find a o7 pivot chord when given two keys; 4) modulation in a slightly different vein: a o7 (or some inversion) turning into a Mm7 (or some inversion); and 5) analysis hints.
- Brief introduction: the versatility of the o7 chord
Consider the following chords:
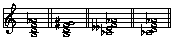
o7 o65 o43 o42
- Given a single o7 chord, one may modulate anywhere
Think for a moment of the chord shown above: B D F Ab and its enharmonic equivalents. If B functions as the root, it may resolve to some sort of C chord--either C major or c minor. If G# functions as the root, it may resolve to some sort of A chord--either A major or a minor. If F functions as the root, it may resolve to some sort of Gb chord--either Gb major or gb minor. If D functions as the root, it may resolve to some sort of Eb chord--either Eb major or eb minor.
Make any sense so far? Reread the previous paragraph until you understand it. Now here's the yet more tricky part: those hypothetical chords of resolution--CM, am, or whatever--don't necessarily have to be a tonic chord in a key. For example, see the progression shown below:
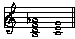
This could function as viio7--I in C major, o7/IV--IV in G major, o7/V--V in F major, or f minor, o7/III--III in a minor, o7/VI--VI in e minor, and so on. The possibilities are thus virtually endless.
Here's what we'll work on next: given a o7 chord of some kind, how could it function in a particular key? There are basically five steps involved:
- Imagine that each note of the o7 may be a root, and think of the pitches that it may resolve to (be sure to include enharmonic equivalents).
- Ask yourself: which of those pitches of resolution are diatonic in the key you're thinking of? (For our purposes, think of natural minor--that is, think of lowered 6 a half-step above 5, and think of the subtonic -- "natural" 7 as found in the key signature).
- Eliminate those pitches which are 7 in a major key, or if your "target key" is minor, eliminate 2. The reason: as you already know, there's no such thing as o7/viio nor o7/iio in a minor key.
- Once you figure out the pitch or pitches left, think of the enharmonic spelling of the o7 needed so that the o7 will resolve to that pitch.
- Make sure that you figure out the correct inversion.
As an example, let's use the o7 chord F# A C Eb and the key of D major.
- F# would resolve to G. A would resolve to Bb (or enharmonically to A#). C would resolve to Db (or enharmonically to C#). Finally, Eb would resolve to Fb (or enharmonically to E).
- The resolution pitches G, C#, and E are diatonic in D major.
- Eliminate C# because it's 7 in D major.
- The chord would thus resolve either to G or to E. To resolve to G, the root needs to be F# and the spelling would thus be F# A C Eb. To resolve to E, the root needs to be D# and the spelling would thus be D# F# A C. The C-naturals are included to make the spelling completely correct--they negate the C-sharp of the key signature.
- Since the "given" chord is F# A C Eb, this would simply function as o7/IV. If you think of the spelling where D# is the root, however, then F# (the "given" root) is really the third of the chord D# F# A C, so the proper inversion is o65/ii.
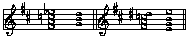
While they may look very different, and are written as different inversions of a o7 chord, THEY SOUND IDENTICAL. These chords are thus enharmonically equivalent.
This means that when you hear this chord, you can't be absolutely sure of what inversion the chord is in, nor what the root of the chord really is (note: some theorists say that o7 chords don't really have "roots." They're really right, but for the purposes of this discussion, we'll make use of the term). Composers (especially those of the late 18th and 19th centuries, especially in developmental sections of music) take advantage of this ambiguity and use the o7 chord as a pivot chord for modulation.
This may all appear to be an intellectual conceit, but it's really not--it can and should affect performance. If you realize that the o7 is a "slippery," ambiguous chord, then you realize that those moments when they are emphasized are moments of musical (and perceptual) ambiguity. The intelligent performer may then elect to "play with" the moments of ambiguity, perhaps giving them just a bit more time or rubato in order to allow the ambiguity to have its fullest effect.
D: o7/IV IV D: o65/ii ii
- Given two keys, how can I find o7 pivot chord(s)?
Compared to what you just did, this is pretty easy. Well, there's really the easy but incomplete way and also the tougher but more comprehensive way. Let's do both, using the somewhat unlikely keys of C major and f# minor.
- the easy/incomplete way. For this, all you do is write out the pitches of both scales (use natural minor for minor keys) and find the notes they have in common. Eliminate 7 in a major key and 2 in a minor key. For CM and f#m, the pitches in common are A, B, D, and E. Eliminate the pitch B since it's 7 in C major, and you'll see that A, D, and E still "work." This means that o7 of A, D, and E would work as a pivot chord: o7/A is /vi in CM and /III in f#m, o7/D is /ii in CM and /VI in f#m, and o7/E is /iii in CM and /bVII in f#m. Notice how the diminished 7th chord may be "of" a major chord in one key and "of" a minor chord in the other--this is O.K.
- the tougher/more comprehensive way. Begin by doing the easy way just
illustrated. Then, there's a second thing to think about: any o7 of any
pitches that are a m3 or tritone apart will also work. Thus, using CM and
f#m, such things as viio7 in CM and viio43 in f# or o7/IV in CM and o65/VI
in f# would also work. These are only two of dozens of possibilities, which
is why this might be characterized as the "tougher/more comprehensive
way."
- A o7 chord turning into a Mm7 chord Here's an interesting fact: if
you take a o7 chord and lower any one of its pitches by a half step, you
come out with a Mm7 chord:

Nineteenth-century composers (and some earlier ones, too) thought that this was an incredibly cool thing: the music could arrive at o7 in some key, and then by altering just one note by a half step, the chord could become a dominant seventh (or even a secondary dominant!) in some new key. This could actually work the other way, too, but this is more rare--take a Mm7 chord, raise its root by a half step, and it becomes a o7 chord.
- Analysis hints What you've read basically covers it, but there are
a few more important points to make:
- This one's especially important: if the o7 pivot just occurs once as a single chord (as is usually the case), then it cannot be spelled two different ways at once. Therefore, it may be spelled "incorrectly" in one of the two keys. While there are no hard-and-fast rules here, it's more often spelled "correctly" in the new key and "incorrectly" in the old one (this makes sense, since the music moves on into the new key, leaving the old one behind).
- This then becomes a matter of interpretation: the Roman numeral function in one of the keys will usually be clear enough, but it will be less clear in the key where it's spelled "incorrectly." In addition, one can't rely on spelling alone--one must consider any and all enharmonic possibilities. So, one then has to be logical: o7 chords usually function as viiox in a key, or as something "of" V or perhaps "of" IV. If the two possibilities are, say, o42/bVII or o65/V, it should be obvious that the chord "of" V makes more sense.
- The chords most often involved probably are viiox and/or ox/V. One additional thing which sometimes happens: composers will occasionally modulate from a major key to its dominant by using o7/ii in the tonic key, then resolving it surprisingly to a major triad which then becomes V of the new key. An example: you're going along in CM, and you encounter a o7/ii chord, which you'd expect to resolve to a d minor chord. It resolves unexpectedly to a D major chord, which then becomes V of G major. Composers often will stick in a I64 in the new key before the V; this is even more of a surprising resolution.
II. The +6 as a pivot chord
In case you haven't noticed yet, the Gr+6 chord is enharmonically equivalent to a dominant seventh chord--they sound identical, though they're spelled differently. Notice in the following examples that the respelling involves the seventh of the dominant seventh chord versus the augmented sixth (the raised 4) of the augmented sixth chord. Another important thing to know: the pivot chord typically only occurs once; it thus can't be spelled both ways. While it could be spelled "correctly" in either the old or the new key, it's probably more often the case that the chord is spelled as it functions in the new key, as was mentioned in the discussion of o7 chords above. While there are a lot of possibilities, we'll focus on two: the V7 becoming a Gr+6 in another key (or the reverse) and V7/IV becoming a Gr+6 in another key (or the reverse).
The V7 becoming the Gr+6 (or the reverse): in this case, the keys will be a minor second apart; the keys may be either major or minor. When the V7 becomes the Gr+6 (which happens more often, since pivot chords are often a pre-dominant chord in the new key), the new key is a half step lower:

C: I IV I64 V I V7 = b:Gr+6 i64 V i
This could just as easily have modulated to B major--the Gr+6 is identical in either b minor or B major.
When the Gr+6 becomes the V7 (a bit less likely than the preceding), the new key will be a half step higher:
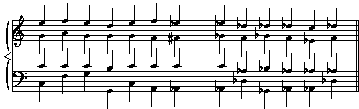
C: I IV I64 V I IV6 Gr+6=Db: V7 I IV I64 V I
The V7/IV becoming the Gr+6 (or the reverse): in this case, the keys will be a major third apart. More often than not, the "old" tonic chord has a minor seventh added to it, thus creating a V7/IV. The latter then functions enharmonically as a Gr+6 in a new key a M3 higher:
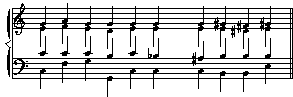
C: I IV I64 V I V7/IV=E:Gr+6 I64 V I
III. The Neapolitan as a pivot chord
This is the simplest topic in the handout. There are two possibilities: either a diatonic chord in the old key becomes a Neapolitan sixth chord in the new key, or the reverse--a Neapolitan sixth chord in the old key becomes a diatonic chord in the new key.
A couple of things to think about:
- since the N6 is a major triad in first inversion, then it's likely to be equivalent to I6, IV6, or V6 in a major key, or III6, V6, or VI6 in a minor key.
- since pivot chords often function as pre-dominant chords in the new key, the RN function of the pivot in the new key is likely to be N6 or IV6. See the examples on the next page.
- Theoretically, it's possible for a secondary dominant of some kind to be involved: for example, the N6 in the old key could become V6/V in the new key. Bear in mind that this is possible, but we will not worry extensively about it in this class.
