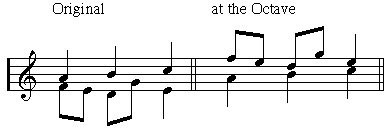
(The following discussion is gleaned from Counterpoint in the Style of J.S. Bach, by Thomas Benjamin)
Double counterpoint is a compositional technique used to ensure that a passage will sound equally satisfactory with either of two voices in the upper position. The use of this technique leads to a consistent thematic content and contrapuntal relationship. Themes are often written in pairs with one voice designated as accompanimental material, such as the subject and countersubject in a fugue. By using double counterpoint, these theme pairs may be freely exchanged between voices while still preserving an acceptable harmonic structure.
Double counterpoint at the octave (or fifteenth) is probably the most common. In this style, the pair of voices can be exchanged at the octave (or a multiple), as seen in the following example.
(click on the musical examples to listen to them.)
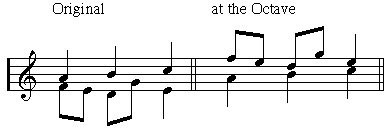
In this example, the lower voice has been transposed up one octave to exchange positions with the upper voice. The same results would be achieved if the upper voice of the original were transposed down one octave (or multiple octaves). In this type of voice exchange, most of the harmonic intervals retain their character (dissonant intervals remain dissonant, imperfect consonances remain imperfect consonances). The one difference is that a perfect fifth inverts to a perfect fourth. Because of that, when writing in double counterpoint at the octave, the fifth must be treated as a dissonant interval (and handled correctly as a non-harmonic tone). The following is a table of intervals for double counterpoint at the octave.
Original: 1 2 3 4 5 6 7 8 Inverted: 8 7 6 5 4 3 2 1
A second common transposition is double counterpoint at the twelfth. In this style, the upper voice may be transposed down one octave, and the lower voice up a perfect fifth (or the lower voice up one octave and the upper voice down a perfect fifth). The following example illustrates one of these possibilities.

With this method, most dissonances remain dissonant and perfect consonances remain perfect. The problem interval is the sixth. When inverted in this manner, the sixth becomes a seventh, and must, therefore, be treated as a dissonance in the original. Following is a table of intervals for double counterpoint at the twelfth.
Original: 1 2 3 4 5 6 7 8 9 10 11 12 Inverted: 12 11 10 9 8 7 6 5 4 3 2 1
The following example, from Invention No. 9 in f minor by J.S. Bach, illustrates the use of double counterpoint at the octave. Note what type of intervals are placed on strong beats, and how dissonant intervals are treated.

